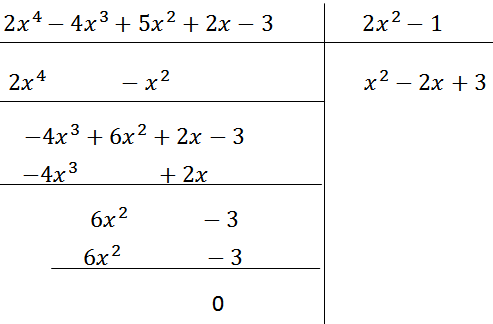Giải bài 1, 2, 3, 4, 5 trang 130, 131 SGK toán 8 tập 2
Giải bài tập trang 130, 131 Ôn tập cuối năm đại số sgk toán 8 tập 2. Câu 1: Phân tích các đa thức sau thành nhân tử:…
Bài 1 trang 130 sgk toán 8 tập 2
Phân tích các đa thức sau thành nhân tử:
a)\({a^2} – {b^2} – 4a + 4;\)
Bạn đang xem: Giải bài 1, 2, 3, 4, 5 trang 130, 131 SGK toán 8 tập 2
b) \({x^2} + 2x – 3\)
c) \(4{x^2}{y^2} – {\left( {{x^2}{y^2}} \right)^2}\)
d) \(2{a^3} – 54{b^3}\) .
Hướng dẫn làm bài:
a) \({a^2} – {b^2} – 4a + 4 \Leftrightarrow {a^2} – 4a + 4 – {b^2}\)
= \({\left( {a – 2} \right)^2} – {b^2} = \left( {a – 2 + b} \right)\left( {a – 2 – b} \right)\)
= \(\left( {a + b – 2} \right)\left( {a – b – 2} \right)\)
b) \({x^2} + 2x – 3 = {x^2} + 2x + 1 – 4\)
=\({\left( {x + 1} \right)^2} – {2^2} = \left( {x + 1 + 2} \right)\left( {x + 1 – 2} \right)\)
=\(\left( {x + 3} \right)\left( {x – 1} \right)\)
c) \(4{x^2}{y^2} – {\left( {{x^2}{y^2}} \right)^2} = {\left( {2xy} \right)^2} – {\left( {{x^2} + {y^2}} \right)^2}\)
= \(\left( {2xy – {x^2} – {y^2}} \right)\left( {2xy + {x^2} + {y^2}} \right)\)
=\( – \left( {{x^2} – 2xy + {y^2}} \right)\left( {{x^2} + 2xy + {y^2}} \right)\)
=\( – {\left( {x – y} \right)^2}{\left( {x + y} \right)^2}\)
d) \(2{a^3} – 54{b^3} = 2\left( {{a^3} – 27{b^3}} \right)\)
=\(2\left[ {{a^3} – {{\left( {3b} \right)}^3}} \right] = 2\left( {a – 3b} \right)\left( {{a^2} + 3ab + 9{b^2}} \right)\).
Bài 2 trang 130 sgk toán 8 tập 2
a)Thực hiện phép chia:
(2x4 – 4x3 + 5x2 + 2x – 3) : (2x2 – 1).
b) Chứng tỏ rằng thương tìm được trong phép chia trên luôn luôn dương với mọi giá trị của x.
Hướng dẫn làm bài:
Vậy \(2\left[ {{a^3} – {{\left( {3b} \right)}^3}} \right] = 2\left( {a – 3b} \right)\left( {2{x^4} – 4{x^4} + 5{x^2} + 2x – 3} \right):\left( {2{x^2} – 1} \right) = {x^2} – 2x + 3\left( {{a^2} + 3ab + 9{b^2}} \right)\)
Vậy \(x \in \left\{ { – 2;1;2;5} \right\}\)
b) Thương tìm được có thể viết:
\({x^2} – 2x + 3 = \left( {{x^2} – 2x + 1} \right) + 2\)
= \({\left( {x – 1} \right)^2} + 2 > 0\) với mọi x
Vậy thương tìm được luôn luôn dương với mọi giá trị của x.
Bài 3 trang 130 sgk toán 8 tập 2
Chứng minh rằng hiệu các bình phương của hai số lẻ bất kì thì chia hết cho 8.
Hướng dẫn làm bài:
Gọi hai số lẻ bất kì là 2a + 1 và 2b + 1 (a, b ∈ Z)
Hiệu bình phương của hai số lẻ đó bằng :
\({\left( {2a{\rm{ }} + {\rm{ }}1} \right)^2}-{\rm{ }}{\left( {2b{\rm{ }} + {\rm{ }}1} \right)^2} = \left( {4{a^2} + {\rm{ }}4a{\rm{ }} + {\rm{ }}1} \right){\rm{ }}-{\rm{ }}\left( {4{b^2} + {\rm{ }}4b{\rm{ }} + 1} \right)\)
\( = \left( {4{a^2} + {\rm{ }}4a} \right){\rm{ }}-{\rm{ }}\left( {4{b^2} + {\rm{ }}4b} \right){\rm{ }} = {\rm{ }}4a\left( {a{\rm{ }} + 1} \right){\rm{ }}-{\rm{ }}4b\left( {b{\rm{ }} + {\rm{ }}1} \right)\)
Vì tích của hai số nguyên liên tiếp luôn chia hết cho 2 nên a(a+1) và b(b+1) chia hết cho 2.
Do đó 4a(a + 1) và 4b(b + 1) chia hết cho 8
4a(a + 1) – 4b(b + 1) chia hết cho 8.
Vậy \({\left( {2a{\rm{ }} + {\rm{ }}1} \right)^2}-{\rm{ }}{\left( {2b{\rm{ }} + {\rm{ }}1} \right)^2}\) chia hết cho 8.
Bài 4 trang 130 sgk toán 8 tập 2
Rút gọn rồi tính giá trị của biểu thức sau tại \(x = – {1 \over 3}\) :
\(\left[ {{{x + 3} \over {{{\left( {x – 3} \right)}^2}}} + {6 \over {{x^2} – 9}} – {{x – 3} \over {{{\left( {x + 3} \right)}^2}}}} \right]\left[ {1:\left( {{{24{x^2}} \over {{x^4} – 81}} – {{12} \over {{x^2} + 9}}} \right)} \right]\)
Hướng dẫn làm bài:
+Ngoặc vuông thứ nhất:
\(\left[ {{{x + 3} \over {{{\left( {x – 3} \right)}^2}}} + {6 \over {{x^2} – 9}} – {{x – 3} \over {{{\left( {x + 3} \right)}^2}}}} \right]{{x + 3} \over {{{\left( {x – 3} \right)}^2}}} + {6 \over {{x^2} – 9}} – {{x – 3} \over {{{\left( {x + 3} \right)}^2}}}\)
\(= {{x + 3} \over {{{\left( {x – 3} \right)}^2}}} + {6 \over {\left( {x – 3} \right)\left( {x + 3} \right)}} – {{x – 3} \over {{{\left( {x + 3} \right)}^2}}}\left[ {1:\left( {{{24{x^2}} \over {{x^4} – 81}} – {{12} \over {{x^2} + 9}}} \right)} \right]\)
\(={{{{\left( {x + 3} \right)}^2} + 6\left( {x – 3} \right)\left( {x + 3} \right) – {{\left( {x – 3} \right)}^2}} \over {{{\left( {x – 3} \right)}^2}{{\left( {x + 3} \right)}^2}}}\)
\(={{{x^3} + 9{x^2} + 27x + 27 + 6{x^2} – 54 – \left( {{x^3} – 9{x^2} + 27x – 27} \right)} \over {{{\left( {x – 3} \right)}^2}{{\left( {x + 3} \right)}^2}}}\)
\(={{24{x^2}} \over {{{\left( {x – 3} \right)}^2}{{\left( {x + 3} \right)}^2}}}\)
\(={{24{x^2}} \over {{{\left( {{x^2} – 9} \right)}^2}}}\)
+Ngoặc vuông thứ hai:
\(1:\left( {{{24{x^2}} \over {{x^4} – 81}} – {{12} \over {{x^2} + 9}}} \right) = 1:\left[ {{{24{x^2}} \over {\left( {{x^2} – 9} \right)\left( {{x^2} + 9} \right)}} – {{12} \over {{x^2} + 9}}} \right]\)
\(=1:\left( {{{24{x^2} – 12\left( {{x^2} – 9} \right)} \over {\left( {{x^2} – 9} \right)\left( {{x^2} + 9} \right)}}} \right)\)
\(=1:{{12{x^2} + 108} \over {\left( {{x^2} – 9} \right)\left( {{x^2} + 9} \right)}}\)
\(=1.{{\left( {{x^2} – 9} \right)\left( {{x^2} + 9} \right)} \over {12{x^2} + 108}}\)
\(={{\left( {{x^2} – 9} \right)\left( {{x^2} + 9} \right)} \over {12{x^2} + 108}}\)
\(={{\left( {{x^2} – 9} \right)\left( {{x^2} + 9} \right)} \over {12\left( {{x^2} + 9} \right)}}\)
\(={{{x^2} – 9} \over {12}}\)
Nên
\(\left[ {{{x + 3} \over {{{\left( {x – 3} \right)}^2}}} + {6 \over {{x^2} – 9}} – {{x – 3} \over {{{\left( {x + 3} \right)}^2}}}} \right]\left[ {1:\left( {{{24{x^2}} \over {{x^4} – 81}} – {{12} \over {{x^2} + 9}}} \right)} \right]\)
\(=\left[ {{{x + 3} \over {{{\left( {x – 3} \right)}^2}}} + {6 \over {{x^2} – 9}} – {{x – 3} \over {{{\left( {x + 3} \right)}^2}}}} \right]{{24{x^2}} \over {{{\left( {{x^2} – 9} \right)}^2}}}.{{{x^2} – 9} \over {12}}\)
\(= {{2{x^2}} \over {{x^2} – 9}}\left[ {1:\left( {{{24{x^2}} \over {{x^4} – 81}} – {{12} \over {{x^2} + 9}}} \right)} \right]\)
Tại \(x = – {1 \over 3}\) giá trị của biểu thức là:
\({{2{{\left( { – {1 \over 3}} \right)}^2}} \over {{{\left( { – {1 \over 3}} \right)}^2} – 9}} = {{2.{1 \over 9}} \over {{1 \over 9} – 9}} = {{{2 \over 9}} \over { – {{80} \over 9}}} = – {1 \over {40}}\)
Bài 5 trang 131 sgk toán 8 tập 2
Chứng minh rằng:
\({{{a^2}} \over {a + b}} + {{{b^2}} \over {b + c}} + {{{c^2}} \over {c + a}} = {{{b^2}} \over {a + b}} + {{{c^2}} \over {b + c}} + {{{a^2}} \over {c + a}}\)
Hướng dẫn làm bài:
Cách 1: Thực hiện phép cộng riêng từng vế:
VT: \(={{{a^2}} \over {a + b}} + {{{b^2}} \over {b + c}}{{{a^2}\left( {b + c} \right)\left( {c + a} \right) + {b^2}\left( {a + b} \right)\left( {c + a} \right) + {c^2}\left( {a + b} \right)\left( {b + c} \right)} \over {\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right)}} + {{{c^2}} \over {c + a}}\)
\(={{{b^2}} \over {a + b}} + {{{c^2}} \over {b + c}} + {{{a^2}} \over {c + a}}\)
Tử bằng:
\(={a^2}\left( {bc + ab + {c^2} + ac} \right) + {b^2}\left( {ac + {a^2} + bc + ab} \right) + {a^2}\left( {ab + ac + {b^2} + bc} \right)\)
\(={a^2}bc + {a^3}b + {a^2}{c^2} + {a^3}c + a{b^2}c + {a^2}{b^2} + {b^3}c + a{b^3} + ab{c^3} + a{c^3} + {b^2}{c^2} + b{c^3}\)
\(={a^3}\left( {b + c} \right) + {a^2}\left( {bc + {b^2} + {c^2}} \right) + a\left( {{b^3} + {c^3} + {b^2}c + b{c^2}} \right) + bc\left( {bc + {b^2} + {c^2}} \right)\left( 1 \right)\) (1)
VP: \(={a^3}\left( {b + c} \right) + {a^2}\left( {bc + {b^2} + {c^2}} \right) + a\left( {{b^3} + {c^3} + {b^2}c + b{c^2}} \right){{{b^2}\left( {b + c} \right)\left( {c + a} \right) + {c^2}\left( {a + b} \right)\left( {c + a} \right) + {a^2}\left( {a + b} \right)\left( {b + c} \right)} \over {\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right)}} + bc\left( {bc + {b^2} + {c^2}} \right)\left( 1 \right)\)
\(={b^2}\left( {bc + ab + {c^2} + ac} \right) + {c^2}\left( {ac + {a^2} + bc + ab} \right) + {a^2}\left( {ab + ac + {b^2} + bc} \right)\)
\(={b^3}c + a{b^3} + {b^2}{c^2} + a{b^2}c + a{c^3} + {a^2}{c^2} + b{c^3} + ab{c^2} + {a^3}b + {a^3}c + {a^2}{b^2} + {a^2}bc\)
\(={a^3}\left( {b + c} \right) + {a^2}\left( {bc + {b^2} + {c^2}} \right) + a\left( {{b^3} + {c^3} + {b^2}c + b{c^2}} \right) + bc\left( {bc + {b^2} + {c^2}} \right)\) (2)
So sánh (1) và (2) ta suy ra vế trái bằng vế phải. Vậy đẳng thức được chứng minh.
Cách 2: Xét hiệu hai vế
\({a^3}\left( {b + c} \right) + {a^2}\left( {bc + {b^2} + {c^2}} \right) + a\left( {{b^3} + {c^3} + {b^2}c + b{c^2}} \right) + bc\left( {bc + {b^2} + {c^2}} \right){{{a^2}} \over {a + b}} – {{{b^2}} \over {a + b}} + {{{b^2}} \over {b + c}} – {{{c^2}} \over {b + c}} + {{{c^2}} \over {c + a}} – {{{a^2}} \over {c + a}}\)
\(={{\left( {a + b} \right)\left( {a – b} \right)} \over {a + b}} – {{\left( {b + c} \right)\left( {b – c} \right)} \over {b + c}} + {{\left( {c + a} \right)\left( {c – a} \right)} \over {c + a}}\)
\(=a – b + b – c + c – a = 0\)
Vậy \({{{a^2}} \over {a + b}} + {{{b^2}} \over {b + c}} + {{{c^2}} \over {c + a}} = {{{b^2}} \over {a + b}} + {{{c^2}} \over {b + c}} + {{{a^2}} \over {c + a}}\)
Nhận xét: Cách 2 nhanh gọn hơn cách 1.
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập