Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp
Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp
Bất đẳng thức Cô-si hay bất đẳng thức AM-GM là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Bài viết hôm nay, THPT Ngô Thì Nhậm sẽ giới thiệu về một số kiến thức cần nhớ về bất đẳng thức Cauchy (Cô si) và một số dạng bài tập thường gặp. Bạn tìm hiểu nhé !
I. LÝ THUYẾT CẦN GHI NHỚ VỀ BẤT ĐẲNG THỨC CÔ-SI
1. Bất đẳng thức Cô-si là gì ?
Bạn đang xem: Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp
Tên đúng của bất đẳng thức này là bất đẳng thức AM-GM. Có nhiều cách để chứng minh bđt này nhưng hay nhất là cách chứng minh quy nạp của Cauchy.
Trong toán học, bất đẳng thức Cauchy là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm được phát biểu như sau:
Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng, và trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
+ Nghĩa là:
– Bất đẳng thức Cô si với 2 số thực không âm:
Dấu “=” xảy ra khi và chỉ khi a = b
– Bất đẳng thức Cô si với n số thực không âm:
Dấu “=” xảy ra khi và chỉ khi
2. Các dạng phát biểu của bất đẳng thức Cô-si
a. Dạng tổng quát của bất đẳng thức Cô-si
Cho là các số thực dương ta có:
– Dạng 1:
– Dạng 2:
– Dạng 3:
– Dạng 4:
– Dạng 5:
Dấu đẳng thức xảy ra khi và chỉ khi
b. Dạng đặc biệt của bất đẳng thức Cô-si
Là các trường hợp đặc biệt của dạng tổng quát ở trên khi n=2, n=3.
c. Một số bất đẳng thức được suy ra từ bất đẳng thức Cauchy
d. Chú ý khi sử dụng bất đẳng thức AM – GM
- Khi áp dụng bất đẳng thức cô si thì các số phải là những số không âm
- Bất đẳng thức côsi thường được áp dụng khi trong BĐT cần chứng minh có tổng và tích
- Điều kiện xảy ra dấu ‘=’ là các số bằng nhau
- Bất đẳng thức côsi còn có hình thức khác thường hay sử dụng
Đối với hai số:
- x2+y2≥2xy.
- x2+y2≥(x+y)22
- xy≤(x+y2)2
Đối với ba số: abc≤a3+b3+c33,abc≤(a+b+c3)3
3. Hệ quả của bất đẳng thức Cô-si
+
+
+
+
+
4. Chứng minh của Cauchy
a. Các trường hợp tất cả các giá trị bằng nhau
Nếu tất cả các giá trị bằng nhau:
tức tổng chúng là nx1, do đó giá trị trung bình cộng là x1; và tích các số dưới căn bậc hai là x1n, do dó giá trị trung bình nhân lúc này là x1; vì vậy, vế một và vế 2 bằng nhau, điều phải chứng minh.
b. Các trường hợp các giá trị không bằng nhau
Nếu tất cả các giá trị bằng nhau không bằng nhau, thì giá trị trung bình cộng lớn hơn giá trị trung bình nhân. Rõ ràng, điều này chỉ có thể xả ra khi n> 1. Trường hợp này khá phức tạp và được chia ra nhiều trường hợp để chứng minh.
c. Trường hợp n = 2
Nếu n= 2, tức có hai giá trị x1 và x2, và từ giả thiết ở trên, ta có:
điều phải chứng minh.
d. Trường hợp n = 2k
Xem xét các trường hợp n= 2 k, với k là một số nguyên dương. Chúng tôi tiến hành bằng quy nạp toán học.
Trong trường hợp cơ bản,k = 1, tức n = 2, bất đẳng thức đã được chứng minh ở trên.
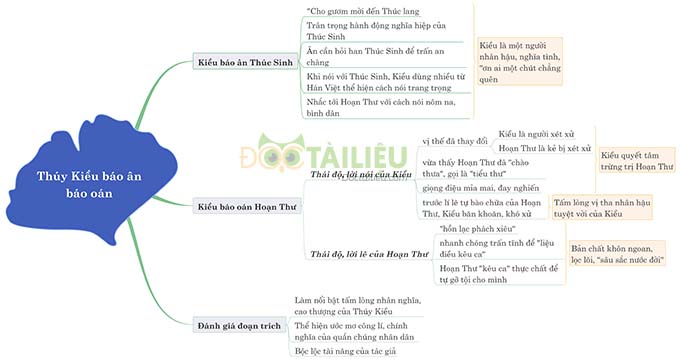
Khi, có một giá trị k> 1 bất kỳ, giả sử rằng bất đẳng thức đúng với n = 2k−1, và cần chứng minh rằng nó vẫn đúng khi n = 2k. Để làm như vậy, các bước được thực hiện như sau:
với bất đẳng thức đầu tiên, hai bên đều bằng nhau chỉ khi cả hai điều sau đây là đúng:
(Trong trường hợp này, trung bình số học thứ nhất và trung bình nhân thứ 1 bằngx1, và tương tự với trung bình số học thứ hai và trung bình nhân thứ 2); và trong bất đẳng thức thứ hai, Hai bên chỉ bằng nhau nếu hai giá trị trung bình bằng nhau. Vì không phải tất cả 2 k đều bằng nhau, không thể cho cả hai bất đẳng thức được đẳng, vì vậy chúng ta biết rằng:
(điều phải chứng minh).
e. Trường hợp n < 2k
Nếu n không phải là một hàm mũ tự nhiên cơ số 2, thì nó chắc chắn là nhỏ hơn một số nào đó theo hàm mũ tự nhiên cơ số 2, vì chuỗi 2, 4, 8,…, 2k,… không bị chặn trên. Do đó, mà không mất tính tổng quát, với m giá trị tuân theo hàm mũ tự nhiên cơ số 2 lớn hơn n.
Vì vậy, nếu ta có n số, thì ta có thể biểu diễn giá trị trung bình cộng α, và được mở rộng như sau:
Chúng tôi sau đó có:
như vậy
điều phải chứng minh.
II. CÁC DẠNG BÀI TẬP THƯỜNG GẶP CỦA BẤT ĐẲNG THỨC CÔ-SI
a. Bài tập có lời giải:
Bài 1: Tìm giá trị nhỏ nhất của biểu thức với x > 0
Lời giải:
Áp dụng bất đẳng thức Cô si cho hai số x > 0 và ta có:
Dấu “=” xảy ra khi và chỉ khi (do x > 0)
Vậy min
Bài 2: Cho x > 0, y > 0 thỏa mãn điều kiện . Tìm giá trị lớn nhất của biểu thức
Lời giải:
Áp dụng bất đẳng thức Cô si cho hai số x > 0, y > 0 ta có:
Lại có, áp dụng bất đẳng thức Cô si cho hai số x > 0, y > 0 ta có:
Dấu “=” xảy ra khi và chỉ khi
Vậy minA = 4 khi và chỉ khi x = y = 4
Bài 3: Chứng minh với ba số a, b, c không âm thỏa mãn a + b + c = 3 thì:
Nhận xét: Bài toán đạt được dấu bằng khi và chi khi a = b = c = 1. Ta sẽ sử dụng phương pháp làm trội làm giảm như sau:
Lời giải:
Áp dụng bất đẳng thức Cô si cho ba số a, b, c không âm có:
Tương tự ta có và
Cộng vế với vế ta có:
Dấu “=” xảy ra khi và chỉ khi a = b = c = 1
b. Bài luyện tập thêm:
Bài 1: Tìm giá trị nhỏ nhất của các biểu thức sau:
a, với x > 0
(gợi ý: biến đổi rồi áp dụng bất đẳng thức Cô si)
b, với x > 0
c, với x > 2
(gợi ý: biến đổi rồi áp dụng bất đẳng thức Cô si)
Bài 2: Tìm giá trị nhỏ nhất của biểu thức với x > y > 0
(gợi ý: biến đổi )
Bài 3: Với a, b, c là các số thực không âm, chứng minh:
(gợi ý áp dụng bất đẳng thức Cô si cho ba số a, b, c không âm)
Bài 4: Cho ba số thực dương a, b, c thỏa mãn a + b + c = 3. Chứng minh rằng:
(gợi ý sử dụng phương pháp làm trội)
Vậy là các em vừa được tìm hiểu lý thuyết và các dạng bài tập thường gặp của bất đẳng thức Cô-si. Hi vọng, chia sr cùng bà viết bạn nắm vững hơn phần kiến thức Đại số 9 vô cùng quan trọng này. Xem thêm các phép biến đổi biểu thức chứa căn thức bậc hai tại đường link này nhé !
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giáo dục




![begin{align} x_1 & ne x_2 \[3pt] x_1 - x_2 & ne 0 \[3pt] left( x_1 - x_2 right) ^2 & > 0 \[3pt] x_1^2 - 2 x_1 x_2 + x_2^2 & > 0 \[3pt] x_1^2 + 2 x_1 x_2 + x_2^2 & > 4 x_1 x_2 \[3pt] left( x_1 + x_2 right) ^2& > 4 x_1 x_2 \[3pt] Bigl( frac{x_1 + x_2}{2} Bigr)^2 & > x_1 x_2 \[3pt] frac{x_1 + x_2}{2} & > sqrt{x_1 x_2} end{align}](https://thptngothinham.edu.vn/wp-content/uploads/2021/12/9410e577cf28a28c506d0e30926da6c2.png)
![begin{align} frac{x_1 + x_2 + cdots + x_{2^k}}{2^k} & {} =frac{frac{x_1 + x_2 + cdots + x_{2^{k-1}}}{2^{k-1}} + frac{x_{2^{k-1} + 1} + x_{2^{k-1} + 2} + cdots + x_{2^k}}{2^{k-1}}}{2} \[7pt] & ge frac{sqrt[2^{k-1}]{x_1 x_2 cdots x_{2^{k-1}}} + sqrt[2^{k-1}]{x_{2^{k-1} + 1} x_{2^{k-1} + 2} cdots x_{2^k}}}{2} \[7pt] & ge sqrt{sqrt[2^{k-1}]{x_1 x_2 cdots x_{2^{k-1}}} sqrt[2^{k-1}]{x_{2^{k-1} + 1} x_{2^{k-1} + 2} cdots x_{2^k}}} \[7pt] & = sqrt[2^k]{x_1 x_2 cdots x_{2^k}} end{align}](https://thptngothinham.edu.vn/wp-content/uploads/2021/12/dba1815ae5a676631bbe679237515771.png)

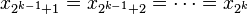

![begin{align} alpha & = frac{x_1 + x_2 + cdots + x_n}{n} \[6pt] & = frac{frac{m}{n} left( x_1 + x_2 + cdots + x_n right)}{m} \[6pt] & = frac{x_1 + x_2 + cdots + x_n + frac{m-n}{n} left( x_1 + x_2 + cdots + x_n right)}{m} \[6pt] & = frac{x_1 + x_2 + cdots + x_n + left( m-n right) alpha}{m} \[6pt] & = frac{x_1 + x_2 + cdots + x_n + x_{n+1} + cdots + x_m}{m} \[6pt] & > sqrt[m]{x_1 x_2 cdots x_n x_{n+1} cdots x_m} \[6pt] & = sqrt[m]{x_1 x_2 cdots x_n alpha^{m-n}},, end{align}](https://thptngothinham.edu.vn/wp-content/uploads/2021/12/bc2e5e9141d6a002a95c74952b8f14ef.png)
![begin{align} alpha^m & > x_1 x_2 cdots x_n alpha^{m-n} \[5pt] alpha^n & > x_1 x_2 cdots x_n \[5pt] alpha & > sqrt[n]{x_1 x_2 cdots x_n} end{align}](https://thptngothinham.edu.vn/wp-content/uploads/2021/12/10ac985e1d4f8088bd50527bb6471adf.png)