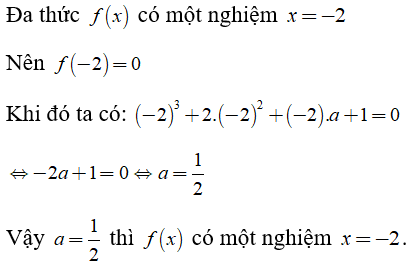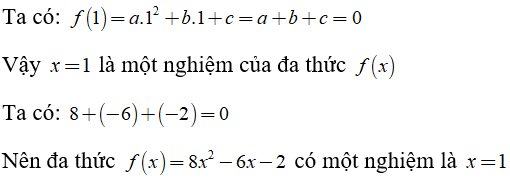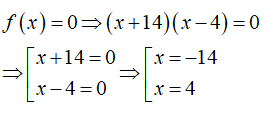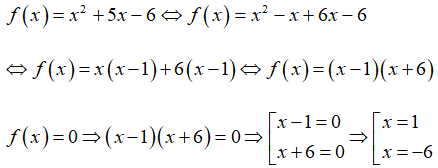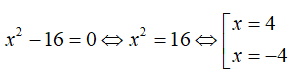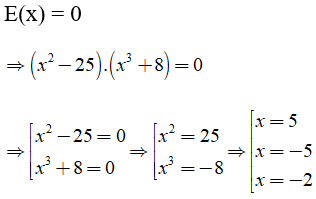Nghiệm của đa thức là gì?
Nếu tại x = a, đa thức P(x) có giá trị bằng 0 thì ta nói a (hoặc x = a) là một nghiệm của đa thức đó.
Ví dụ 1: Kiểm tra xem mỗi số 1; 2; -1 có phải là một nghiệm của đa thức f(x) = x2 – 3x + 2 hay không?
Ví dụ 2: Cho đa thức f(x) = x3 + 2x2 + ax + 1
Tìm a biết rằng đa thức f(x) có một nghiệm x = -2
Chú ý:
+ Một đa thức (khác đa thức không) có thể có một nghiệm, hai nghiệm,… hoặc không có nghiệm.
+ Số nghiệm của một đa thức (khác đa thức không) không vượt quá bậc của nó. Chẳng hạn: đa thức bậc nhất chỉ có một nghiệm, đa thức bậc hai không quá hai nghiệm,…
Ví dụ 3: Tìm nghiệm của đa thức P(x) = 2y + 6
Từ 2y + 6 = 0 ⇒ 2y = -6 ⇒ y = -6/2 = -3
Vậy nghiệm của đa thức P(x) là -3.
Ví dụ 4: Giả sử a, b, c là các hằng số sao cho a + b + c = 0. Chứng minh rằng đa thức f(x) = ax2 + bx + c có một nghiệm là x = 1 . Áp dụng để tìm một nghiệm của đa thức f(x) = 8x2 – 6x – 2.
Bài tập về nghiệm của đa thức một biến có đáp án
Bài 1: Cho đa thức f(x) = 2x2 + 12x + 10. Trong các số sau, số nào là nghiệm của đa thức đã cho:
A. -9
B. 1
C. -1
D. -4
f(-9) = 2.(-9)2 + 12.(-9) + 10 = 64 ≠ 0 ⇒ x = -9 không là nghiệm của f(x)
f(1) = 2.(1)2 + 12.(1) + 10 = 24 ≠ 0 ⇒ x = 1 không là nghiệm của f(x)
f(-1) = 2.(-1)2 + 12.(-1) + 10 = 0 ⇒ x = 1 là nghiệm của f(x)
f(-4) = 2.(-4)2 + 12.(-4) + 10 = -6 ≠ 0 ⇒ x = -4 không là nghiệm của f(x)
Chọn đáp án C
Bài 2: Cho các giá trị của x là 0; -1; 1; 2; -2. Giá trị nào của x là nghiệm của đa thức P(x) = x2 + x – 2
A. x = 1; x = -2
B. x = 0; x = -1; x = -2
C. x = 1; x = 2
D. x = 1; x = -2; x = 2
P(0) = 02 + 0 – 2 = -2 ≠ 0 ⇒ x = 0 không phải là nghiệm của P(x)
P(-1) = (-1)2 + 1.(-1) – 2 = -2 ≠ 0 ⇒ x = -1 không là nghiệm của P(x)
P(1) = 12 + 1.1 – 2 = 0 ⇒ x = 1 là nghiệm của P(x)
P(2) = 22 + 1.2 – 2 = 4 ≠ 0 ⇒ x = 2 không là nghiệm của P(x)
P(-2) = (-2)2 + 1.(-2) – 2 = 0 ⇒ x = -2 không là nghiệm của P(x)
vậy x = 1; x = -2 là nghiệm của P(x)
Chọn đáp án A
Bài 3: Tập nghiệm của đa thức f(x) = (x + 14)(x – 4) là:
A. {4; 14}
B. {-4; 14}
C. {-4; -14}
D. {4; -14}
Vậy tập nghiệm của đa thức f(x) là {4; -14}
Chọn đáp án D
Bài 4: Cho đa thức sau f(x) = x2 + 5x – 6. Các nghiệm của đa thức đã cho là:
A. 2 và 3
B. 1 và – 6
C. -3 và -6
D. -3 và 8
Vậy nghiệm của đa thức f(x) là 1 và -6
Chọn đáp án B
Bài 5: Tổng các nghiệm của đa thức x2 – 16 là:
A. -16
B. 8
C. 4
D. 0
Vậy x = 4; x = -4 là nghiệm của đa thức x2 – 16
Tổng các nghiệm là 4 + (-4) = 0
Chọn đáp án D
Bài 6: Số nghiệm của đa thức x3 + 27 là:
A. 1
B. 2
C. 0
D. 3
Ta có x3 + 27 = 0 ⇒ x3 = -27 ⇒ x3 = (-3)3 ⇒ x = -3
Vậy đa thức đã cho có một nghiệm x = -3
Chọn đáp án A.
Bài 7: Số nào sau đây là nghiệm của đa thức M(x) = x2 – 18x + 81
A. 6
B. 7
C. 8
D. 9
Chọn đáp án D
Bài 8: Hai số nào trong bốn số -1; -3; 1; 3 là nghiệm của đa thức H(x) = x2 – 2x – 3
A. -1 và 1
B. -3 và 3
C. -1 và 3
D. 1 và -3
Chọn đáp án C
Bài 9: Cho đa thức G(x) = x2 + 5. Khẳng định nào sau đây là đúng?
A. G(x) không có nghiệm
B. G(x) có một nghiệm
C. G(x) có hai nghiệm
D. A, B, C đều sai
Vì x2 ≥ 0 ⇒ x2 + 5 ≥ 5 ≥ 0
Do đó đa thức G(x) = x2 + 5 không có nghiệm.
Chọn đáp án A
Bài 10: Nghiệm của đa thức E(x) = (x2 – 25).(x3 + 8) là
A. 5 và -5
B. 5; -5 và -2
C. 5; -5 và 2
D. -2 và 2
Vậy nghiệm của đa thức E(x) là 5; -5 và -2
Chọn đáp án B
********************
Đăng bởi: Trường THPT Ngô Thì Nhậm
Chuyên mục: Giáo dục
