Giáo dục
06/07/2023
Bài 2 trang 174 SGK Ngữ văn 9 tập 1
Tài liệu hướng dẫn trả lời câu hỏi bài 2 trang 174 SGK Ngữ văn 9 tập 1 phần trả lời câu hỏi…
Giáo dục
06/07/2023
Bài 3 trang 143 SGK Ngữ văn 9 tập 2
Tài liệu hướng dẫn trả lời câu hỏi bài 3 trang 143 sách giáo khoa Ngữ văn 9 tập Hai…
Giáo dục
06/07/2023
Bài 1 trang 174 SGK Ngữ văn 9 tập 1
Hướng dẫn chi tiết trả lời bài 1 trang 174 SGK Ngữ văn lớp 9 tập 1 phần trả lời…
Giáo dục
06/07/2023
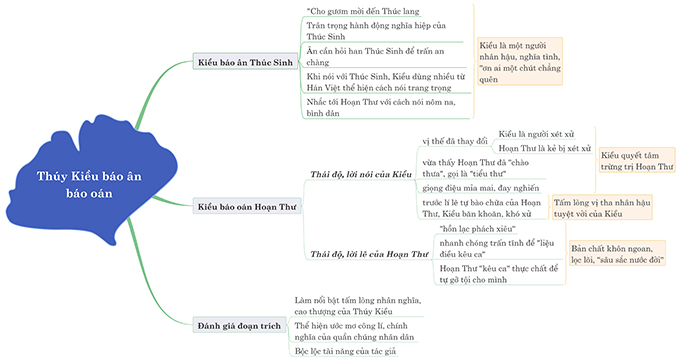
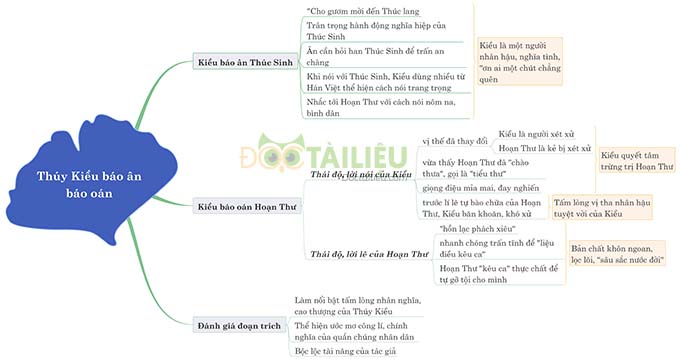
Cảm nhận đoạn trích Thúy Kiều báo ân báo oán
THPT Ngô Thì Nhậm hướng dẫn cảm nhận đoạn trích Thúy Kiều báo ân báo oán, gợi ý cách làm, lập dàn…
Giáo dục
06/07/2023
Bài 2 trang 143 SGK Ngữ văn 9 tập 2
Hướng dẫn chi tiết trả lời bài 2 trang 143 sách giáo khoa ngữ văn lớp 9 tập 2 phần…
Giáo dục
06/07/2023
Bài 2 trang 157 SGK Ngữ văn 9 tập 1
Tài liệu hướng dẫn trả lời câu hỏi bài 2 trang 157 SGK Ngữ văn 9 tập 1 phần trả lời câu hỏi…
Giáo dục
06/07/2023
Nêu cảm nghĩ về nhân vật Xi-mông trong truyện ngắn Bố của Xi-mông
Có thể muốn xem qua bài văn phân tích tác phẩm Bố của Xi-mông của Guy đơ Mô-pa-xăng để hiểu…
Giáo dục
06/07/2023
Bài 3 trang 157 SGK Ngữ văn 9 tập 1
Hướng dẫn chi tiết trả lời bài 3 trang 157 SGK Ngữ văn lớp 9 tập 1 phần trả lời…
Giáo dục
06/07/2023
Tóm tắt Rô bin xơn ngoài đảo hoang của Đi-phô
Tóm tắt Rô bin xơn ngoài đảo hoang của Đi-phô để vẽ nên hình ảnh một Rô bin xơn dũng…
Giáo dục
06/07/2023
Bài 1 trang 157 SGK Ngữ văn 9 tập 1
Hướng dẫn chi tiết trả lời bài 1 trang 157 SGK Ngữ văn lớp 9 tập 1 phần trả lời…